productos notables (lo que vamos viendo en matematicas)

binomio al cuadrado o cuadrado de un binomio

Ilustración gráfica del binomio al cuadrado.

Para elevar un binomio al cuadrado (es decir, multiplicarlo por sí mismo), se suman los cuadrados de cada término con el doble del producto de ellos. Es decir:

un trinomio de la forma: , se conoce como trinomio cuadrado perfecto.
Cuando el segundo término es negativo, la ecuación que se obtiene es:

En ambos casos el tercer término tiene siempre signo positivo.

Ejemplo

simplificando:

Producto de dos binomios con un término común

Ilustración gráfica del producto de binomios con un término común

Cuando se multiplican dos binomios que tienen un término común, se suma el cuadrado del término común con el producto el término común por la suma de los otros, y al resultado se añade el producto de los términos diferentes.

Ejemplo

agrupando términos:

luego:

Producto de dos binomios conjugados

Véase también: Conjugado (matemática)

Producto de binomios conjugados.

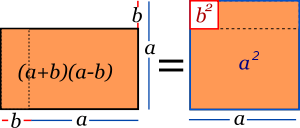
Dos binomios conjugados son aquellos que sólo se diferencien en el signo de la operación. Para multiplicar binomios conjugados, basta elevar los monomios al cuadrado y restarlos, obteniendo una diferencia de cuadrados

Ejemplo

agrupando términos:

A este producto notable también se le conoce como suma por la diferencia.

Polinomio al cuadrado

Elevando un trinomio al cuadrado de forma gráfica

Para elevar un polinomio con cualquier cantidad de términos, se suman los cuadrados de cada término individual y luego se añade el doble de la suma de los productos de cada posible par de términos.

Ejemplo

multiplicando los monomios:

agrupando términos:

luego:

Binomio al cubo o cubo de un binomio

Descomposición volumétrica del binomio al cubo

Para calcular el cubo de un binomio, se suma: el cubo del primer término, con el triple producto del cuadrado del primero por el segundo, más el triple producto del primero por el cuadrado del segundo, más el cubo del segundo término.

Identidades de Cauchy:

Ejemplo

agrupando términos:

Cuando la operación del binomio es resta, el resultado es: el cubo del primer término, menos el triple producto del cuadrado del primero por el segundo, más el triple producto del primero por el cuadrado del segundo, menos el cubo del segundo término.

Identidades de Cauchy:

Ejemplo

agrupando términos:

¿QUE ES EL INTERNET?

Internet es el legado del sistema de protección de los Estados Unidos para mantener sus computadoras militares conectadas en caso de un ataque militar y la destrucción de uno o varios de los nodos de su red de computadoras.
En la actualidad es una enorme red que conecta redes y computadoras distribuidas por todo el mundo, permitiéndonos comunicarnos y buscar y transferir información sin grandes requerimientos tecnológicos ni económicos relativos para el individuo.
En esta red participan computadoras de todo tipo, desde grandes sistemas hasta modelos personales descontinuados hace años. En adición, se dan cita en ella instituciones gubernamentales, educativas, científicas, sin fines de lucro y, cada vez más, empresas privadas con intereses comerciales, haciendo su información disponible a un público de más de 30 millones de personas.

 Orígenes

Internet tuvo un origen militar que puede rastrearse a 1969, cuando la Agencia de Proyectos para Investigación Avanzada (Advanced Research Projects Agency en inglés ó ARPA) del Departamento de Defensa de los Estados Unidos conectó cuatro sistemas de cómputos geográficamente distantes en una red que se conoció como ARPAnet.
Pero, si bien la idea original estaba intrínsecamente ligada a la seguridad militar, su evolución e implementación tuvieron lugar alrededor del mundo académico. La misma red en experimentación sirvió para conectar a los científicos desarrollándola y ayudarlos a compartir opiniones, colaborar en el trabajo y aplicarla para fines prácticos. Pronto, ARPAnet conectaría todas las agencias y proyectos del Departamento de Defensa de los E.U.A. y para 1972 se habían integrado ya 50 universidades y centros de investigación diseminados en los Estados Unidos.
Eventualmente la Fundación Nacional de Ciencia (National Science Foundation en inglés ó NSF), entidad gubernamental de los Estados Unidos para el desarrollo de la ciencia se hizo cargo de la red, conectando las redes que luego darían lugar a la red de redes que hoy llamamos Internet.